牛客在线编程大厂笔试模考

更新中……

知识点-动态规划

VC1 牛牛吃草

牛牛吃草

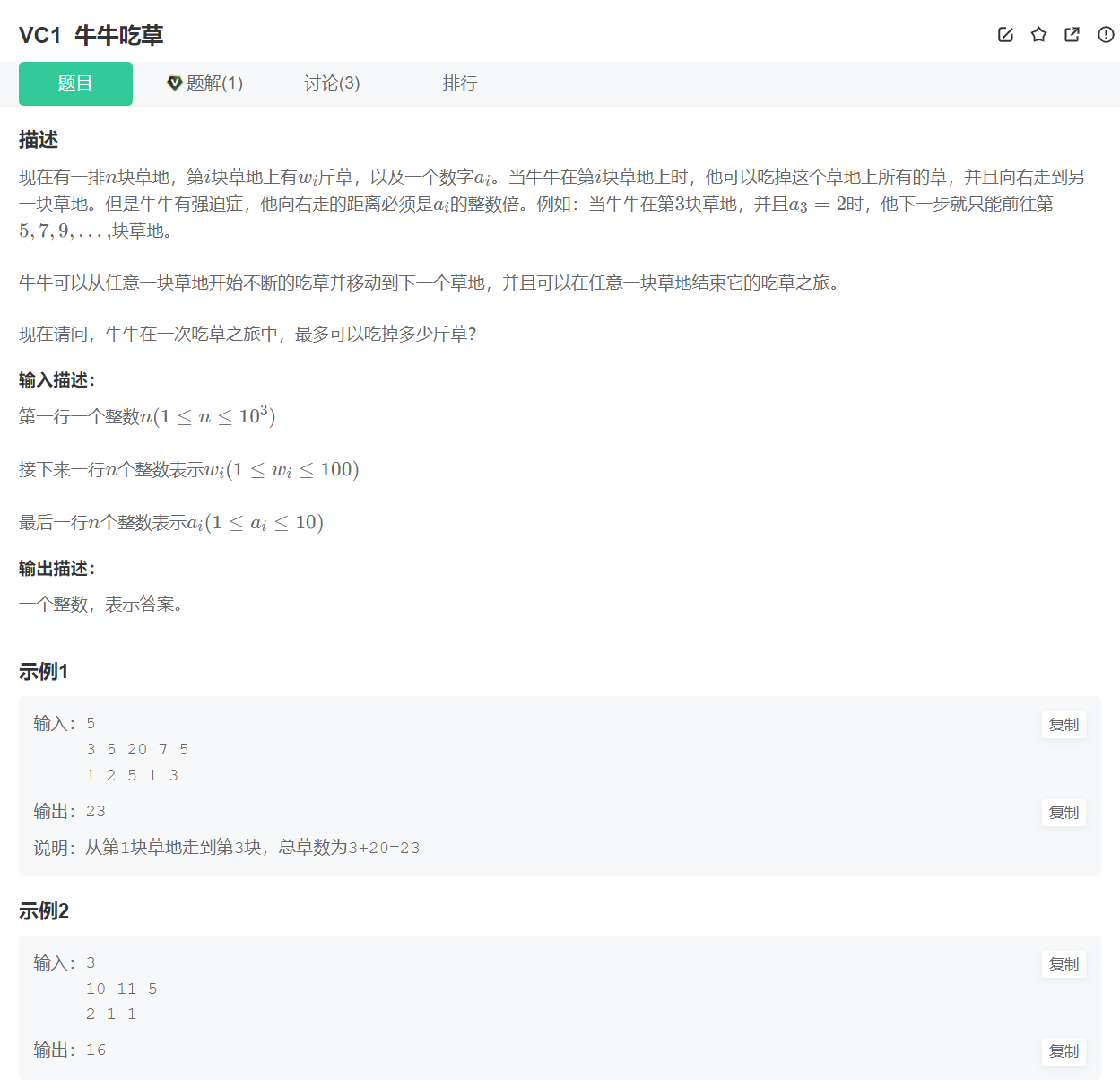
代码

/*
输入：
5
3 5 20 7 5
1 2 5 1 3
输出：
23
*/
#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;
    vector<int> W(n);
    vector<int> A(n);
    
    for(int i = 0; i < n; ++i) {
        cin >> W[i];
    }
    
    for(int i = 0; i < n; ++i) {
        cin >> A[i];
    }
    
    vector<int> dp(n);
    dp[n-1] = W[n-1];
    
    int res = dp[n-1];
    for(int i = n - 2; i >= 0; --i) {
        int maxn = 0;
        for(int j = i + A[i]; j < n; j += A[i]) {
            maxn = max(maxn, dp[j]);
        }
        dp[i] = W[i] + maxn;
        res = max(dp[i], res);
    }
    
    cout << res;
    return 0;
}

知识点-记忆化搜索

VC2 棋盘

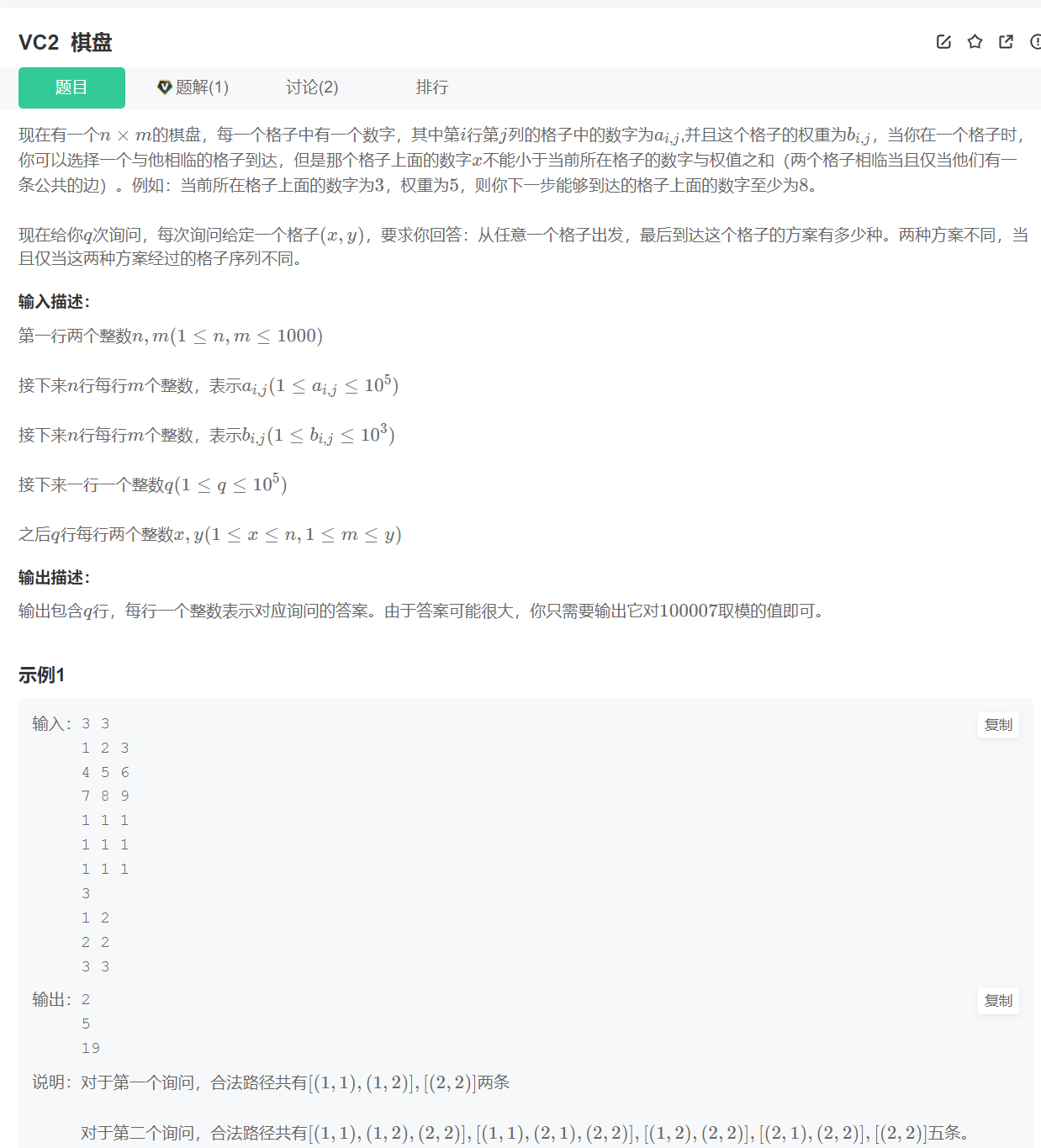
代码

思路：逆向思维

/*
输入：
3 3
1 2 3
4 5 6
7 8 9
1 1 1
1 1 1
1 1 1
3
1 2
2 2
3 3
输出：
2
5
19
*/
# include <bits/stdc++.h>

using namespace std;

const int MOD = 100007;
const int direction[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int n, m, q;
int dfs(vector<vector<int>> &A, vector<vector<int>> &B, vector<vector<int>> &record, int x, int y){
    if(x < 0 || x >= n || y < 0 || y >= m){
        return 0;
    }
    if(record[x][y]){
        return record[x][y];
    }
    record[x][y] = 1;

    int cnt = 0;
    for(int i = 0; i < 4; ++i) {
        int pre_x = x + direction[i][0];
        int pre_y = y + direction[i][1];
        if(pre_x >= 0 && pre_x < n && pre_y >= 0 && pre_y < m && A[pre_x][pre_y] + B[pre_x][pre_y] <= A[x][y]) {
            record[x][y] += dfs(A, B, record, pre_x, pre_y); // 前一步能到达该点的路径数
        }
    }
    record[x][y] % MOD;
    return record[x][y];
}

int main() {

//     freopen("test.txt", "r", stdin);
    cin >> n >> m;
    vector<vector<int>> A(n, vector<int>(m));
    vector<vector<int>> B(n, vector<int>(m));
    
    for(int i = 0; i < n; ++i) {
        for(int j = 0; j < m; ++j) {
            cin >> A[i][j];
        }
    }
    
    for(int i = 0; i < n; ++i) {
        for(int j = 0; j < m; ++j) {
            cin >> B[i][j];
        }
    }
    
    cin >> q;
    
    vector<vector<int>> record(n, vector<int>(m, 0)); // record[i][j] 存储能到达该点的点的路径数
    while(q--) {
        // code
        int x, y;
        cin >> x >> y; // 注意 x y 下标从 1 开始
        --x;
        --y;
        cout << dfs(A, B, record, x, y) << endl;
        
    }
}

知识点-差分

VC3 涂颜料

涂颜料

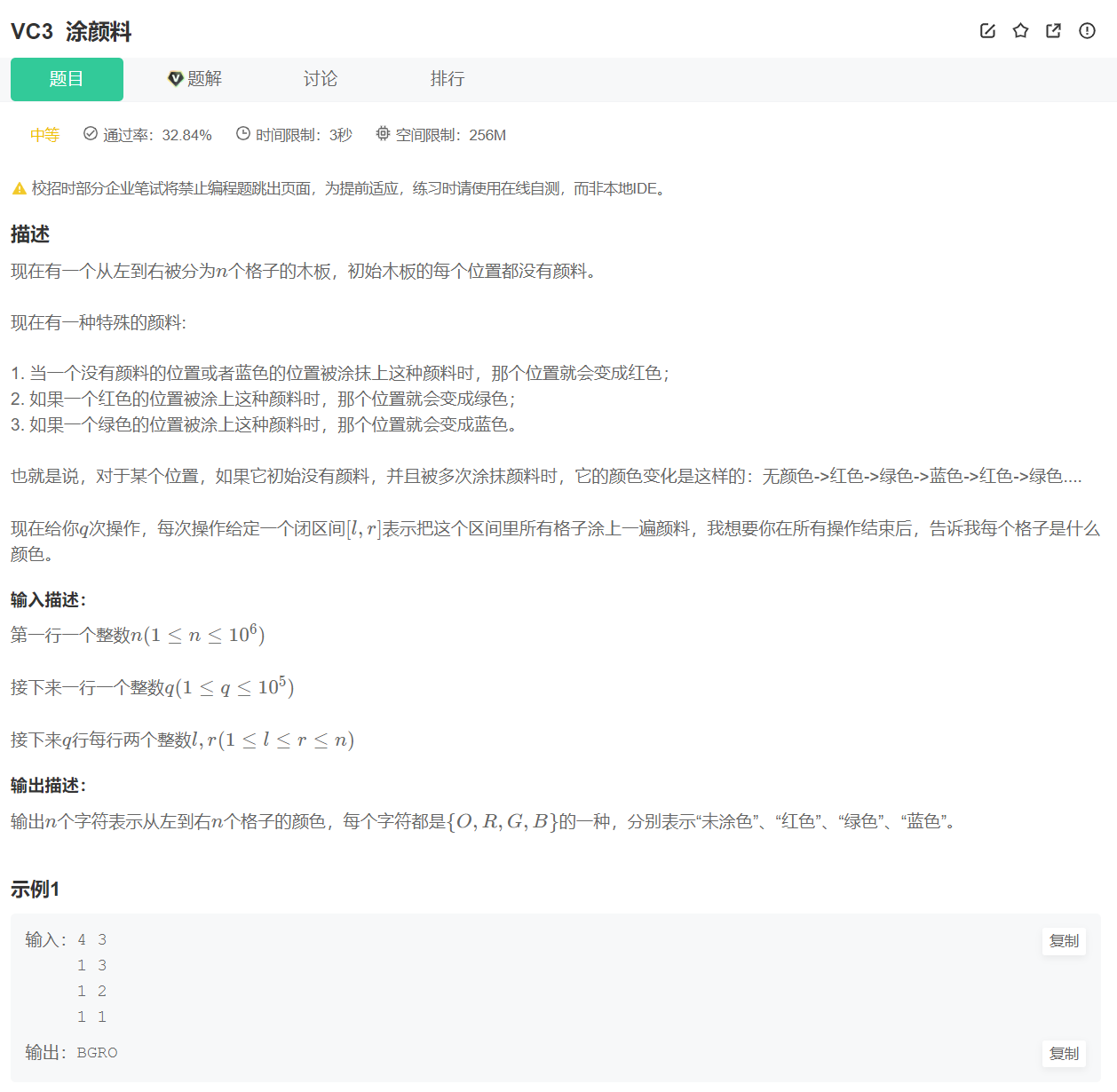
LeetCode 类似的题： 370. 区间加法 - 力扣（LeetCode）

代码

/*
输入：
4 3
1 3
1 2
1 1
输出：
BGRO
*/
#include <bits/stdc++.h>
using namespace std;

char color[3] = {'R', 'G', 'B'};

int main() {
    // freopen("test.in", "r", stdin);
    int n, q;
    cin >> n >> q;

    vector<int> vec(n, 0);
    while (q--)
    {
        int l, r;
        cin >> l >> r;
        --l; // 牛客的题每次都是下标从1开始，我是真的会谢
        --r;
        vec[l] += 1;
        vec[r + 1] -= 1;
    }

    for (int i = 0; i < n; ++i) {
        if(i > 0) {
            vec[i] += vec[i - 1];
        }

        if(vec[i] == 0) {
            printf("O");
        } else {
            printf("%c", color[(vec[i]-1)%3]);
        }
    }

    return 0;
}

知识点-拓扑排序

VC4 相遇

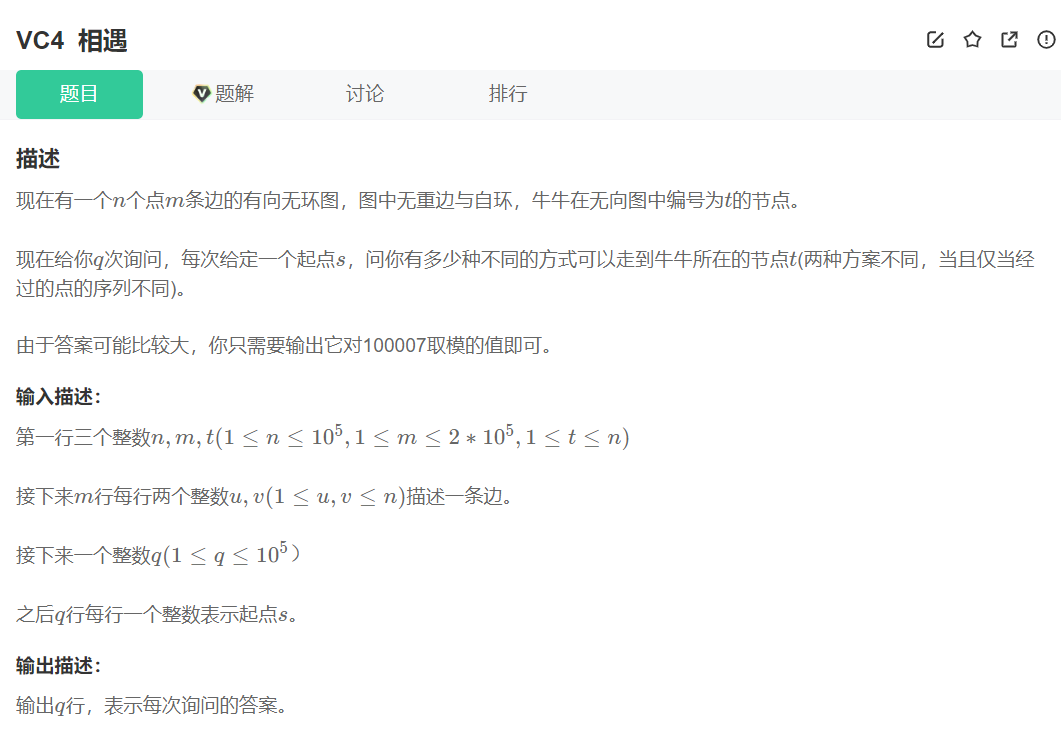
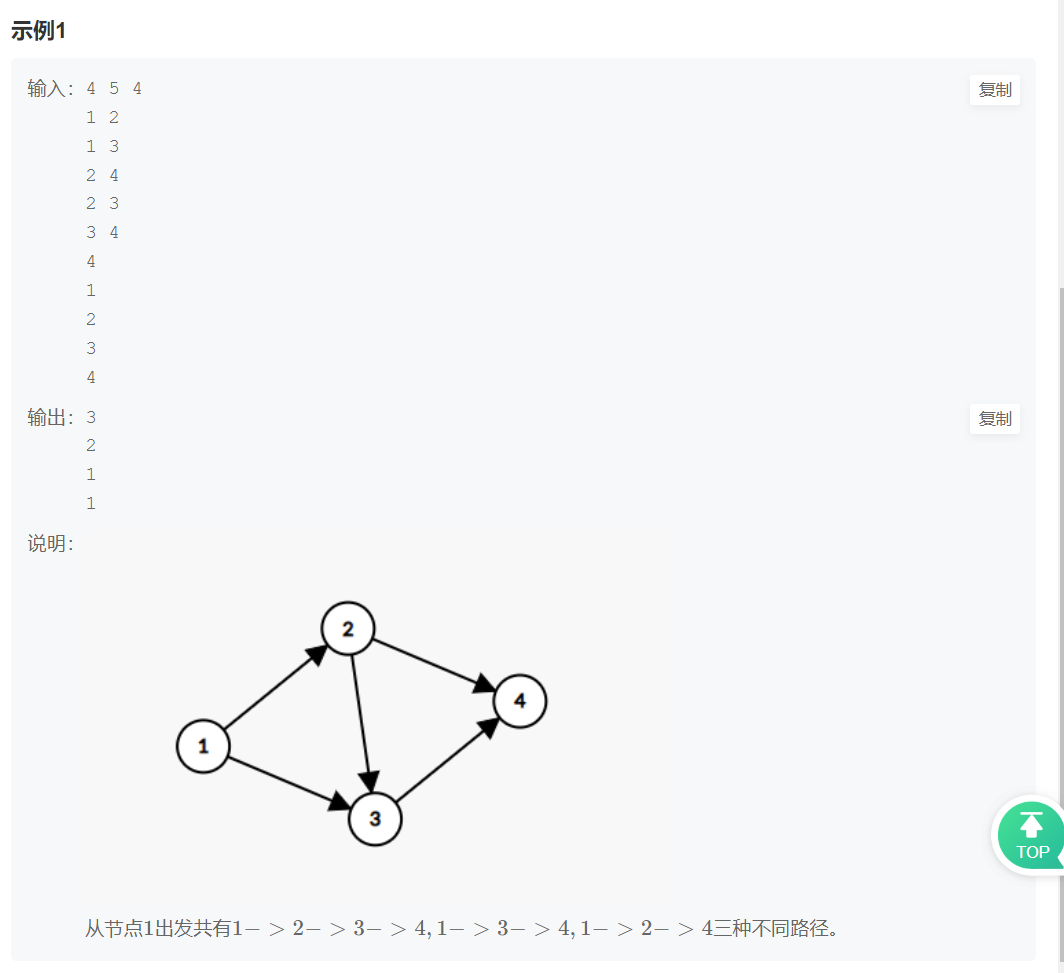
拓扑排序：

有向图的拓扑排序（Topological Sort）是其顶点的线性排序，使得对于从顶点 u 到顶点 v 的每个有向边 uv，u 在排序中都在 v 之前。

例如，图形的顶点可以表示要执行的任务，并且边可以表示一个任务必须在另一个任务之前执行的约束；在这个应用中，拓扑排序只是一个有效的任务顺序。

如果且仅当图形没有定向循环，即如果它是有向无环图（DAG），则拓扑排序是可能的。

DAG

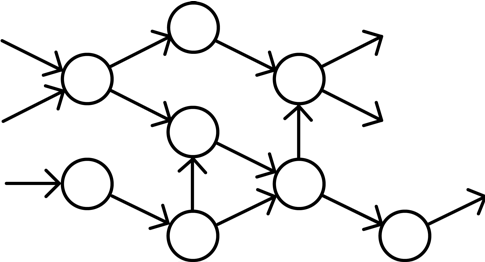
任何 DAG 具有至少一个拓扑排序，存在算法用于在线性时间内构建任何 DAG 的拓扑排序。

代码

dfs超时了。

#include<bits/stdc++.h>

using namespace std;

const int MOD = 100007;
int n, m, t, q;
unordered_map<int, int> record;
vector<vector<int>> graph;
int dfs(int v)
{
    
    if(record.find(v) != record.end()) {
        return record[v];
    }

    int cnt = 0;
    for (int i = 0; i < graph[v].size(); ++i) {
        cnt += dfs(graph[v][i]);
    }

    record[v] = cnt % MOD;
    return cnt;
}

int main()
{
    // freopen("test.in", "r", stdin);
    cin >> n >> m >> t;
    record[t] = 1;
    graph.resize(n + 1);
    while (m--)
    {
        int u, v;
        cin >> u >> v;
        graph[u].emplace_back(v);
    }

    cin >> q;

    while (q--)
    {
        int s;
        cin >> s;
        cout << dfs(s) << endl;
    }
}

bfs：

#include<bits/stdc++.h>

using namespace std;

const int MOD = 100007;
int n, m, t, q;
vector<vector<int>> graph;
vector<int> ind;
stack<int> stk;

int main()
{
    freopen("test.in", "r", stdin);
    cin >> n >> m >> t;
    graph.resize(n + 1);
    ind.resize(n + 1);

    while (m--)
    {
        int u, v;
        cin >> u >> v;
        graph[u].emplace_back(v);
        ++ind[v]; // 统计入度
    }
    queue<int> que;
    stack<int> sorted;
    for (int i = 1; i <= n; ++i)
    {
        if(ind[i] == 0) // 入度为0的点加入队列
            que.emplace(i);
    }

    while (!que.empty())
    {
        int u = que.front();
        que.pop();
        sorted.emplace(u); // 已排序的点
        for (int v : graph[u])
        {
            if(--ind[v] == 0) {// u的下一跳入度减一，入度为0的点加入队列
                que.emplace(v);
            }
        }
    }

    vector<int> dp(n + 1);
    dp[t] = 1;
    while (!sorted.empty())
    {
        int u = sorted.top();
        sorted.pop();
        for (int v : graph[u]) { // 能到达该点的个数为 能达到上一跳点的个数之和
            dp[u] = (dp[u] + dp[v]) % MOD;
        }
    }

    cin >> q;
    while (q--)
    {
        int s;
        cin >> s;
        cout << dp[s] << endl;
    }
}

知识点-并查集

VC5 信号覆盖

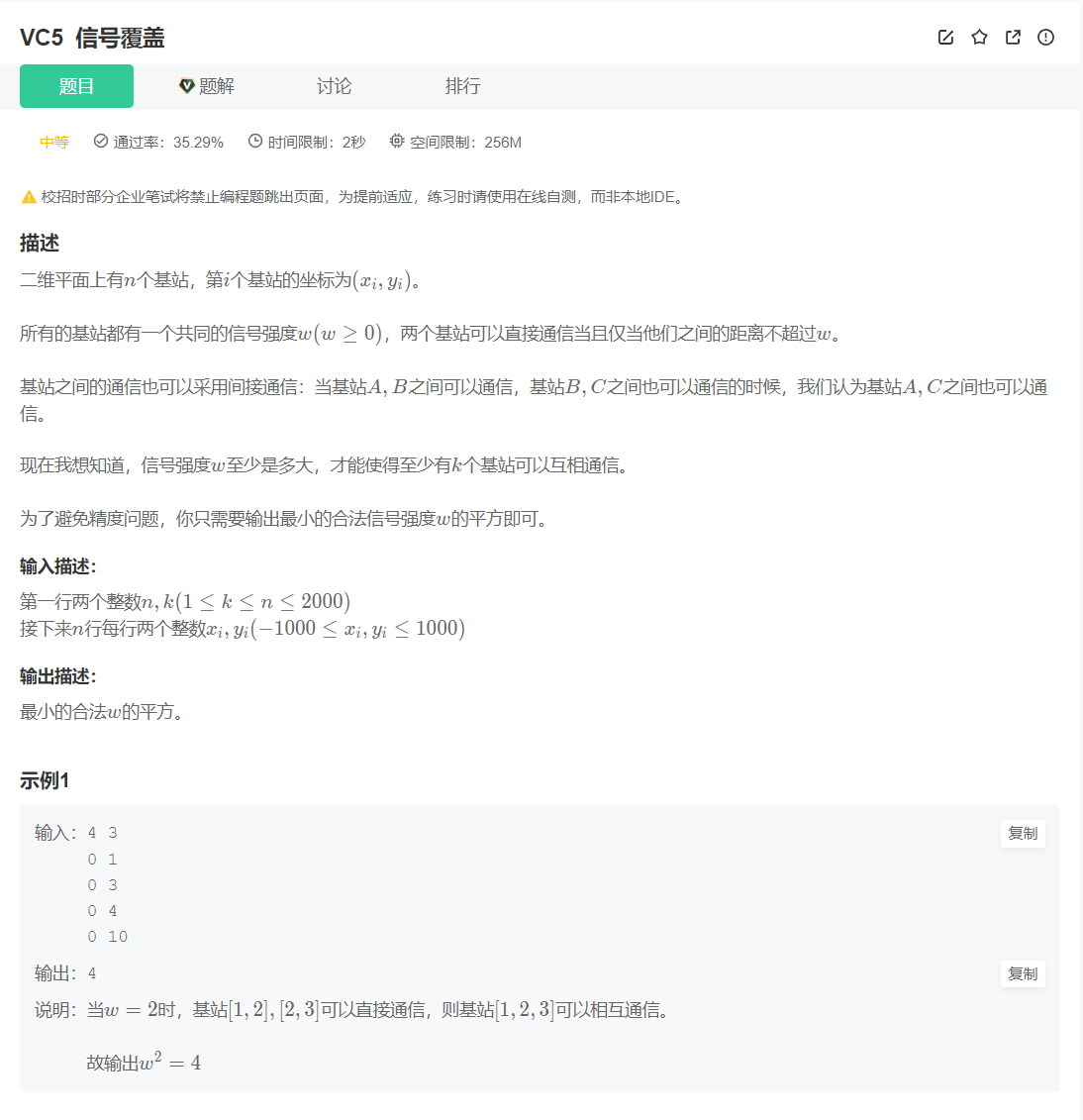
并查集：

并查集（Union-find Data Structure）是一种树型的数据结构。它的特点是由子结点找到父亲结点，用于处理一些不交集（Disjoint Sets）的合并及查询问题。

Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
Union：将两个子集合并成同一个集合。

代码

/*
输入：
4 3
0 1
0 3
0 4
0 10
输出：

4
*/
#include <bits/stdc++.h>
using namespace std;

vector<int> father;

int find(int x) {
    return father[x] == x ? x : father[x] = find(father[x]);
}

int main() {
    // freopen("test.in", "r", stdin);
    int n, k;
    cin >> n >> k;

    if(k == 1) { // k = 1 时，w = 0. 基站自己与自己通信
        printf("0\n");
        return 0;
    }

    vector<pair<int,int>> points(n);
    father.resize(n);

    for (int i = 0; i < n; ++i) {
        cin >> points[i].first >> points[i].second;
    }

    vector<vector<int>> edges;
    for (int i = 0; i < n; ++i)
    {
        for (int j = i + 1; j < n; ++j) {
            int dis = (points[i].first - points[j].first) * (points[i].first - points[j].first) + (points[i].second - points[j].second) * (points[i].second - points[j].second);
            edges.emplace_back(vector<int>{i, j, dis});
        }
    }

    sort(edges.begin(), edges.end(), [](vector<int>& a, vector<int>& b) { 
        return a[2] < b[2]; 
    });

    
    vector<int> sz(n, 1);

    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }

    for (auto e : edges)
    {
        int p = find(e[0]);
        int q = find(e[1]);
        if(p ^ q) { // p != q // 合并两个集合
            father[p] = q; // p 的 根节点改为 q
            sz[q] += sz[p]; 
            if(sz[q] >= k) {
                printf("%d\n", e[2]);
                return 0;
            }
        }
    }
    return 0;
}

知识点-单调栈

VC6 愤怒的小鸟

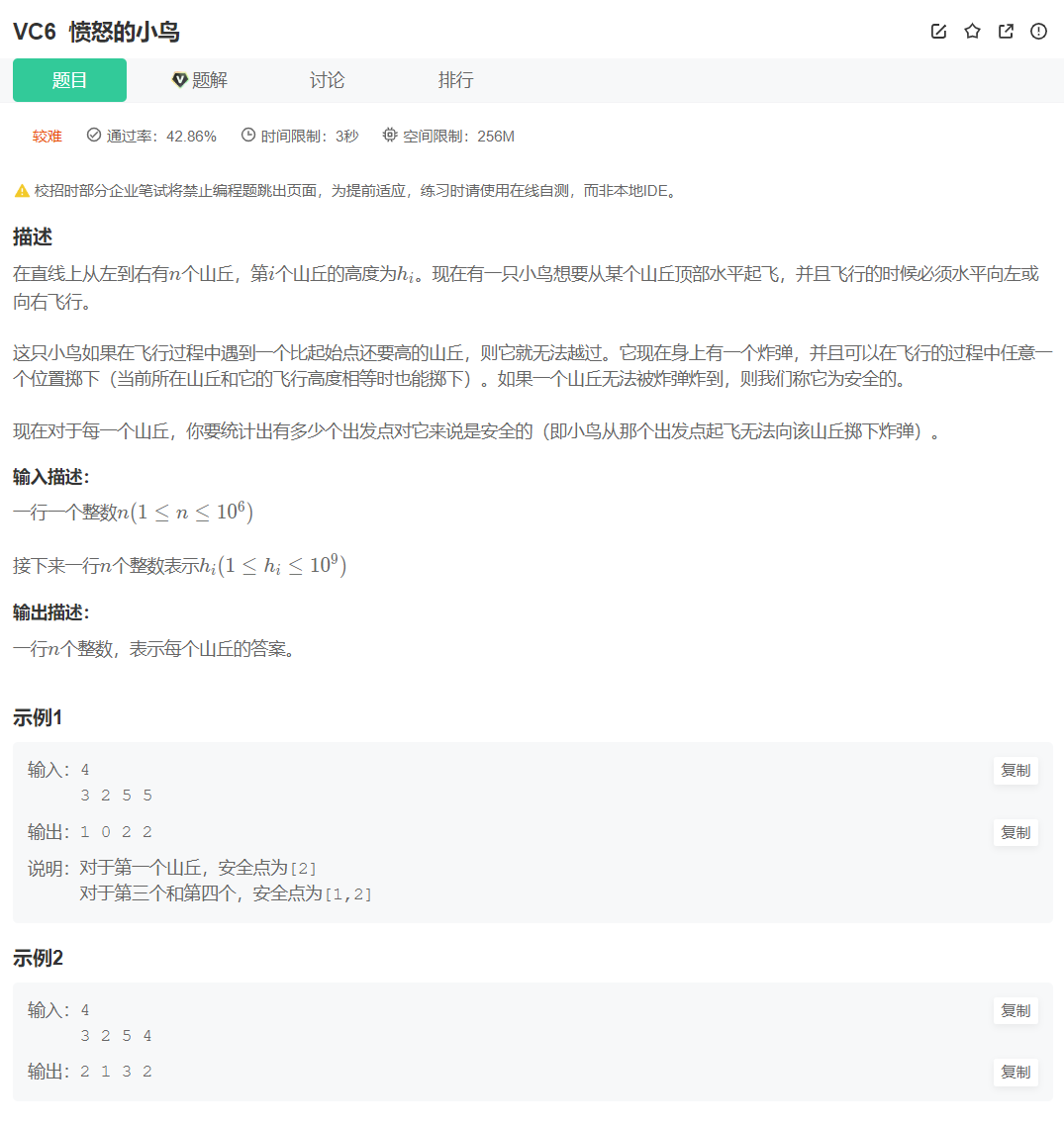
代码

#include<bits/stdc++.h>

using namespace std;

int main() {
    int n;
    cin >> n;
    vector<int> height(n);

    for (int i = 0; i < n; ++i) {
        cin >> height[i];
    }

    stack<int> stk; // 单调栈，递减栈，表示可达到该点的山的个数
    vector<int> L(n);
    vector<int> R(n);

    for (int i = 0; i < n; ++i)
    {
        while (!stk.empty() && stk.top() < height[i])
        {
            stk.pop();
        }
        L[i] = stk.size();
        stk.emplace(height[i]);
    }

    stack<int>().swap(stk);
    for (int i = n - 1; i >= 0; --i)
    {
        while (!stk.empty() && stk.top() < height[i])
        {
            stk.pop();
        }
        R[i] = stk.size();
        stk.emplace(height[i]);
    }

    for (int i = 0; i < n; ++i)
    {
        printf("%d ", (n - 1 - L[i] - R[i]));
    }
    return 0;
}